Split Methods & Hyperparameter Tuning

Introduction

Resolution bushes, a elementary software in machine studying, are used for each classification and regression. With every inner node representing a call primarily based on a function and every leaf node representing an end result, determination bushes mirror human decision-making processes, making them accessible and interpretable. Their versatility in dealing with each numerical and categorical knowledge has made them indispensable throughout varied domains equivalent to finance, healthcare, and advertising and marketing. It acts as the bottom for extra complicated algorithms like Random Forest, XGBoost, and LightGBM.

Studying Aims

Acquire a deep understanding of determination bushes, together with theoretical foundations equivalent to customary deviation discount, info achieve, Gini impurity, and chi-square.
Develop sensible proficiency in implementing determination tree fashions utilizing Python and scikit-learn, with step-by-step steering and code explanations.
Study to make use of hyperparameter tuning for determination bushes to optimize parameters equivalent to most depth and minimal samples break up, enhancing mannequin efficiency and generalization capabilities.

Anatomy of Resolution Tree

Root Node: High most node within the Resolution Tree. Represents your entire dataset. 
Inner node: Nodes which might be within the Resolution Tree that aren’t lead nodes AKA Resolution nodes. 
Leaf Node: Terminal node in Resolution tree which represents the ultimate end result. 
Resolution Rule: The trail from root node to the lead node. Consists of a collection of situations.
Splitting criterion: Criterion which is used to find out the partition of the dataset. 

Totally different Resolution Tree Algorithms

ID3(Iterative Dichotomiser 3):  The algorithm constructs a multiway tree by iteratively choosing, in a grasping vogue, the specific function for every node that maximizes info achieve with respect to categorical targets. Timber are expanded till their most measurement is reached, adopted by a pruning step geared toward enhancing the tree’s capability to generalize to new knowledge.

C4.5:  an development over ID3, eliminates the constraint of categorical options by dynamically defining discrete attributes primarily based on numerical variables, partitioning steady attribute values into intervals. It transforms the educated bushes from the ID3 algorithm into units of if-then guidelines. The accuracy of every rule is assessed to find out their sequence of utility. Pruning includes eradicating a rule’s precondition if its accuracy improves with out it.

C5.0: the newest model launched by Quinlan, makes use of decreased reminiscence and generates smaller rule units in comparison with C4.5, all whereas attaining greater accuracy.

CART(Classification and Regression Timber): This shares similarities with C4.5, however diverges by accommodating numerical goal variables for regression duties and omitting the computation of rule units. As an alternative, CART builds binary bushes by choosing the function and threshold mixture that maximizes info achieve at every node.

Sklearn makes use of an optimized model of CART, Sklearn implementation doesn’t assist categorical variables for now. 

What’s Resolution Node Splitting?

A call tree is constructed top-down from a root node and includes partitioning the info into subsets that include cases with comparable values (homogenous). We will probably be utilizing Normal Deviation Discount for steady goal variables and Gini, Data Acquire and Chi-square for categorical goal variables.

What’s Normal Deviation Discount(SDR) ?

We use customary deviation to calculate the homogeneity of a numerical pattern. If the numerical pattern is totally homogeneous its customary deviation is zero.

Steps concerned in Normal Deviation Discount together with an instance dataset:

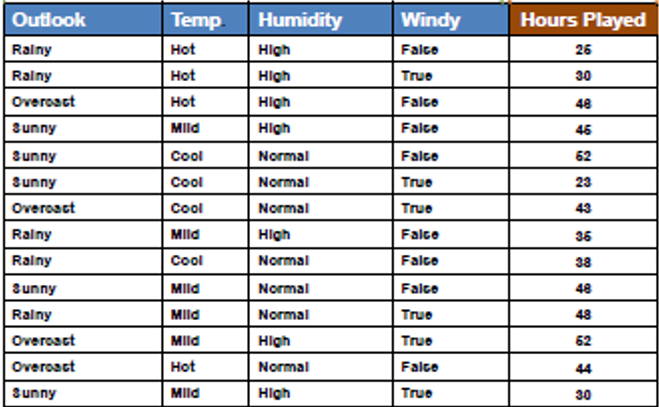
Step 1: Calculate the Normal Deviation (SD) for the Guardian Node(Goal Variable)

Compute the usual deviation of the goal variable (or the variance, as each are proportional) for the info factors within the present node. This represents the impurity or variability of the goal variable throughout the node.

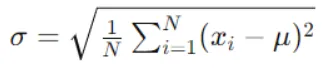
Step 2: Consider Normal Deviation for Every Characteristic

Decide the affect of splitting knowledge on every function on the usual deviation of the goal variable. Compute the usual deviation for every baby node ensuing from the break up and discover the weighted common.

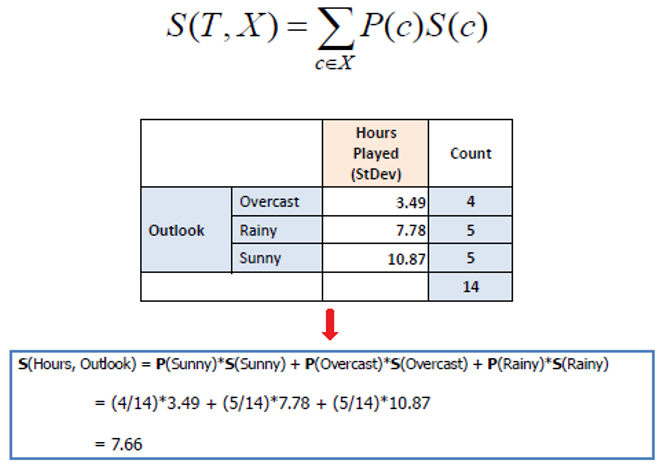
Equally compute for different options as nicely. 

Step 3: Compute Normal Deviation Discount (SDR)

Subtract the weighted common of kid node customary deviations from the guardian node customary deviation. This worth represents the discount in customary deviation achieved by splitting on a function.

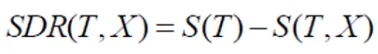
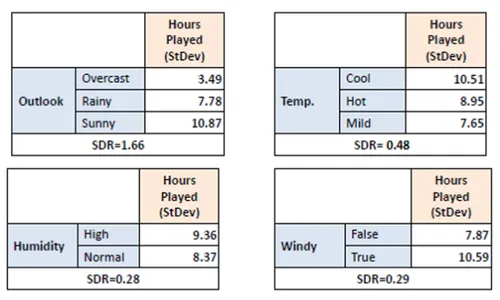
Step 4: Choose Characteristic with Most SDR

Evaluate SDR values for all options. Select the function with the very best discount in customary deviation because the splitting criterion.

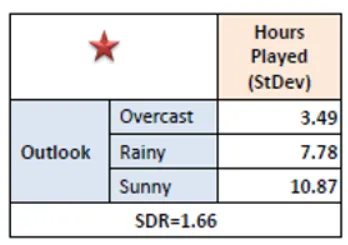
Step 5: Repeat Recursively

Cut up the dataset primarily based on the chosen function into baby nodes. Repeat the method recursively for every baby node till stopping standards are met.

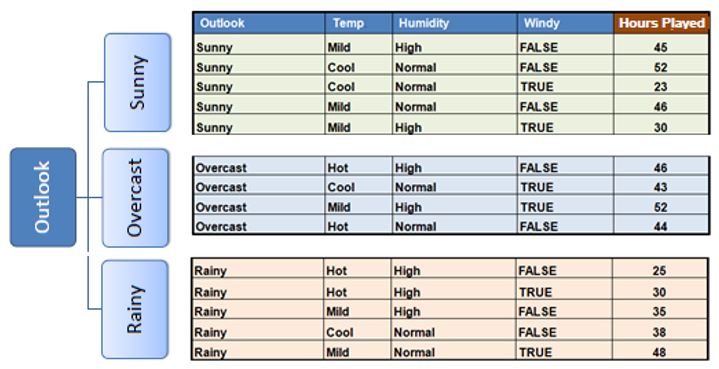
In observe we want some termination standards, we use coefficient of deviation(CV) and variety of knowledge factors in our subset. Often a threshold of 10% is ready for CV and the minimal variety of knowledge factors wanted is 3.  

After discovering the function for the choice node, if the function is categorical then we break up the choice node primarily based on the courses current in that function. If the function is steady then we observe the under steps to search out the optimum break up level. 

Step 1: Type the Characteristic Values: Organize the function in ascending order. 

Step 2: Iterate by way of the options

For every distinctive function worth (excluding the final worth):

Compute the discount in SD by splitting the dataset into two teams:

Group 1: Cases with function values lower than or equal to the present worth.
Group 2: Cases with function values better than the present worth.

Calculate the SD for every group. Compute the weighted common of the SDs for each teams primarily based on the variety of cases in every group. Subtract the weighted common from the SD of the guardian node to acquire the discount in SD.

Step 3: Discover the Optimum Cut up Level

Determine the break up level that yields the utmost discount in SD. This break up level represents the optimum threshold for dividing the continual function into two subsets

Step 4: Cut up the Dataset

Cut up the dataset primarily based on the chosen break up level into two teams:

Group 1: Cases with function values lower than or equal to the break up level.
Group 2: Cases with function values better than the break up level.

Notice: In sklearn library we are able to see that the criterion “squared error” has the implementation just like Normal Deviation Discount. 

What’s Data Acquire(IG)?

IG quantifies the discount in entropy (or uncertainty) achieved by splitting the info on a selected function. Primarily, it measures how way more ordered the info turns into after the break up in comparison with earlier than. A better info achieve signifies that splitting the info on a specific function ends in extra homogeneous subsets with respect to the goal variable. 

Steps concerned in Data Acquire together with an pattern dataset:

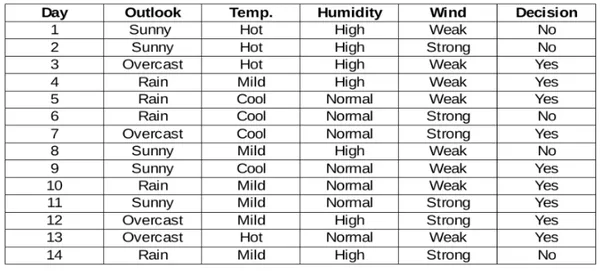
Step 1: Calculate Entropy for the Guardian Node

Compute the entropy of the goal variable for the info factors within the present node, representing uncertainty or impurity. Entropy measures the uncertainty or impurity of a dataset. For a given node S with n courses, entropy is calculated as:

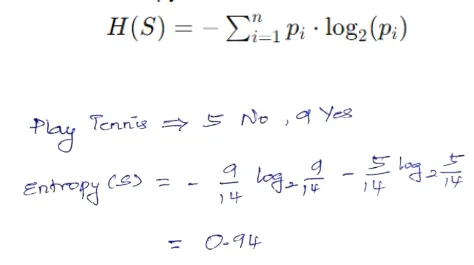
Step 2: Consider Data Acquire for Every Characteristic

Assess the discount in entropy achieved by splitting the info on every function. Compute the entropy for every baby node ensuing from the break up and discover the weighted common.

Data achieve quantifies the discount in entropy achieved by splitting the info on a specific function. The formulation for info achieve is:

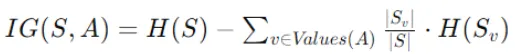
IG(S,A) is the knowledge achieve for splitting node S utilizing function A.
H(S) is the entropy of node S earlier than the break up.
Values(A) characterize the distinct values of function A.
∣Sv∣ is the variety of cases in node S with worth v for function A.
∣S∣ is the full variety of cases in node S.
H(Sv)is the entropy of the subset Sv of cases in node S with worth v for function A.

Equally compute Data achieve for different options as nicely. 

Step 3: Compute Data Acquire

Subtract the weighted common of kid node entropies from the guardian node entropy. This worth represents the knowledge achieve obtained by splitting on a function.

Step 4: Choose Characteristic with Most Data Acquire

Evaluate info achieve values for all options. Select the function with the very best info achieve because the splitting criterion.

Step 5: Repeat Recursively

Cut up the dataset primarily based on the chosen function into baby nodes. Repeat the method recursively for every baby node till stopping standards are met.

What’s Gini Index?

The Gini index, also referred to as the Gini impurity, is a measure of impurity or inequality steadily utilized in determination tree algorithms, particularly for classification duties. It quantifies the chance of incorrectly classifying a randomly chosen ingredient in a dataset.

Steps concerned in Gini Index with the instance as Data achieve:

Step 1: Calculate Gini Index for the Guardian Node

Compute the Gini index of the goal variable for the info factors within the present node, representing impurity. Gini index is calculated as follows:

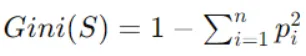
The place pi is the likelihood of sophistication i in node S

Step 2: Consider Gini Index for Every Characteristic

Assess the discount in Gini index achieved by splitting the info on every function. Compute the Gini index for every baby node ensuing from the break up.

Step 3: Compute Gini Index Discount

Subtract the weighted common of kid node Gini indices from the Gini index of the guardian node. This worth represents the discount in Gini index obtained by splitting on a function.

Step 4: Choose Characteristic with Most Gini Index Discount

Evaluate Gini index discount values for all options. Select the function with the very best discount in Gini index because the splitting criterion.

Since we’ve got GI of Outlook to be much less we select it as the basis node. 

Step 5: Repeat Recursively

Cut up the dataset primarily based on the chosen function into baby nodes. Repeat the method recursively for every baby node till stopping standards are met.

What’s Chi-square Check?

Chi-square check is a statistical technique used for function choice. It assesses the independence between attributes (options) and the goal variable. Particularly, the chi-square check evaluates whether or not there’s a vital affiliation between a categorical function and the goal variable in a dataset.

Steps concerned in Chi-square Check:

Step 1: Calculate Contingency Desk

Assemble a contingency desk (also referred to as a cross-tabulation desk) that summarizes the frequency of occurrences for every mixture of function values and sophistication labels.

Step 2: Compute Anticipated Frequencies

Calculate the anticipated frequencies for every cell within the contingency desk underneath the belief of independence between the function and the goal variable. That is achieved by multiplying the row and column totals and dividing by the grand whole of observations.

Anticipated Frequency (E) formulation for a cell with row whole (R) and column whole (C) is:

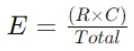
Step 3: Calculate Chi-Sq. Statistic

Compute the Chi-Sq. statistic for every cell utilizing the noticed and anticipated frequencies. The formulation for the Chi-Sq. statistic for a cell is:

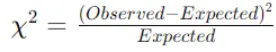
Sum the Chi-Sq. values throughout all cells to acquire the full Chi-Sq. statistic for the function.

Step 4: Decide Levels of Freedom

Decide the levels of freedom (df) for the Chi-Sq. check, which is calculated as:

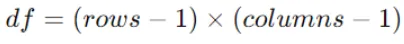
The place rows and columns are the variety of classes within the function and the goal variable, respectively.

Now that we’ve got seen the strategies to separate the Resolution tree we’ll now have a look at the implementation of these. 

For Detailed clarification of Chi Sq., Please Refer CHAID.

What’s Hyper parameter tuning?

Now let’s strive some hyper parameter tuning on the choice tree. The objective from this hyper parameter tuning is to generalize the mannequin and interpret determination bushes at each level. 

Step 1: Importing vital libraries

import numpy as np 
import pandas as pd 
import matplotlib.pyplot as plt 
import seaborn as sns
%matplotlib inline

Step 2: Importing our dataset.

We will probably be utilizing Titanic dataset which is a preprocessed and encoded dataset. 

knowledge = pd.read_csv(“data_cleaned.csv”)
knowledge.head()

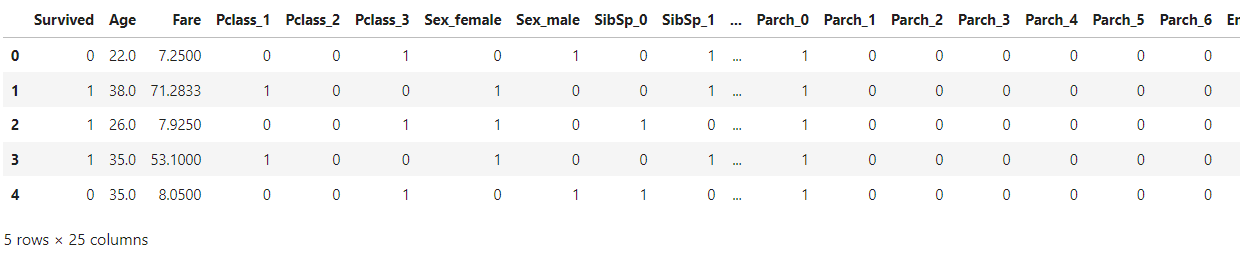
Step 3: Now we’ll break up the options and goal variable

X = knowledge.drop([‘Survived’], axis=1)
knowledge[‘Survived’] = knowledge[‘Survived’].astype(str)
y = knowledge[‘Survived’]

Step 4: Utilizing sklearn’s train_test_split technique

We are going to break up the info into coaching and testing.

Deciding on the ratio is determined by the dataset measurement, if in case you have a big dataset a smaller portion of the dataset will be allotted to check then again with a smaller dataset you need to allocate sufficient knowledge within the check for analysis of the mannequin’s efficiency. Right here for simplicity we’ll use 75% prepare  25% check break up. 

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size = 0.25, random_state = 42)
X_train.information()

Step 5: Import the Resolution Tree mannequin from sklearn

We are going to import the Resolution Tree mannequin from sklearn. Then prepare our mannequin with X_train and y_train. We are going to use random_state = 0 for the reason that randomness of the estimator. The options are all the time randomly permuted at every break up, even when splitter is ready to “greatest”.

from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(random_state=0)
clf.match(X_train, y_train)

Step 6: Analysis on our Resolution Tree classifier

Now lets strive some analysis on our Resolution Tree classifier, Beneath code will give us the confusion matrix. 

from sklearn.metrics import confusion_matrix
confusion_matrix = confusion_matrix(y_test, y_pred_ti)
print(“Confusion Matrix:n”, confusion_matrix)

Step 7:  Discovering Accuracy of Mannequin

We are going to discover the coaching accuracy and testing accuracy of our mannequin. 

clf.rating(X_train, y_train), clf.rating(X_test, y_test)

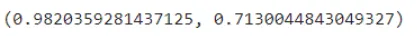
We get our coaching accuracy to be round 98%. and our mannequin bought an accuracy of 71.3% which could be very much less in comparison with our coaching accuracy. Therefore now we will probably be doing a little hyper parameter tuning to our dataset so as to get a generalized mannequin. 

That is our determination tree earlier than any hyper parameter tuning

from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

# Visualize the choice tree
plt.determine(figsize=(20,10)) # Regulate the determine measurement as wanted
plot_tree(clf, crammed=True, feature_names=X_train.columns.tolist(),
class_names=clf.classes_.tolist())
plt.present()

Code to know some info on DT:

import matplotlib.pyplot as plt
tree_info = clf.tree_
num_nodes = tree_info.node_count
num_leaves = tree_info.n_leaves
num_decision = num_nodes – num_leaves

print(“Variety of nodes:”, num_nodes)
print(“Variety of leaves:”, num_leaves)
print(“Variety of determination:”, num_decision)

Step 8: Implement Hyper Parameters of Resolution Timber

Let’s implement some hyper parameters of Resolution Timber. Let’s strive the max_depth parameter as this has the very best affect on our determination tree. max_depth permits the tree to develop deeper, because the tree grows deeper it captures intricate relationships within the knowledge main to raised efficiency. Nevertheless, it additionally will increase the chance of overfitting, because the mannequin memorizes the coaching knowledge as an alternative of generalizing. 

We are going to begin with max_depth = 3 and enhance it accordingly. This acts like a regularization you impose constraints on the mannequin’s complexity because the deeper determination tree will get extra complicated the mannequin turns into. 

clf = DecisionTreeClassifier(max_depth = 3, random_state=0)
clf.match(X_train, y_train)
clf.rating(X_train, y_train), clf.rating(X_test, y_test)

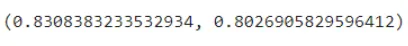
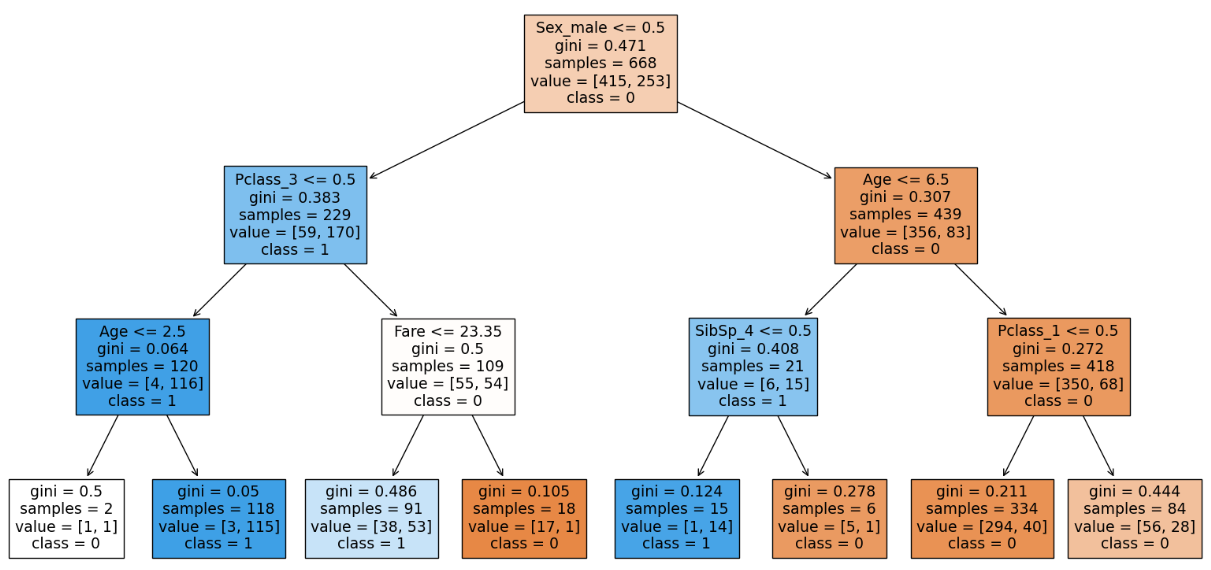
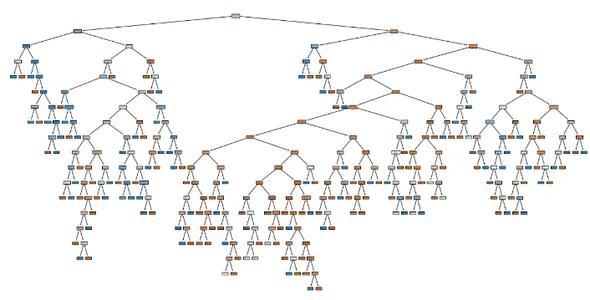
From our visualization we are able to see that 4 out of 8 of the leaf node comprises proportions of our dataset. Therefore we’ve got to go deeper to seize extra relationships. Therefore we’ll enhance the depth to 4. 

We are able to see that the mannequin is extra generalized. Rising depth greater than 4 causes the mannequin to overfit. After max_depth = 4 we are able to see that the mannequin is overfitted. 

Step 9: Making an attempt Hyper Parameter

Now we’ll check out the opposite hyper parameter min_samples_split. As a thumb rule we are able to begin with min_sample_split with 2 or 3 and enhance till the mannequin’s efficiency drops.

clf = DecisionTreeClassifier(max_depth = 4, min_samples_split = 15, random_state=0)
clf.match(X_train, y_train)
clf.rating(X_train, y_train), clf.rating(X_test, y_test)

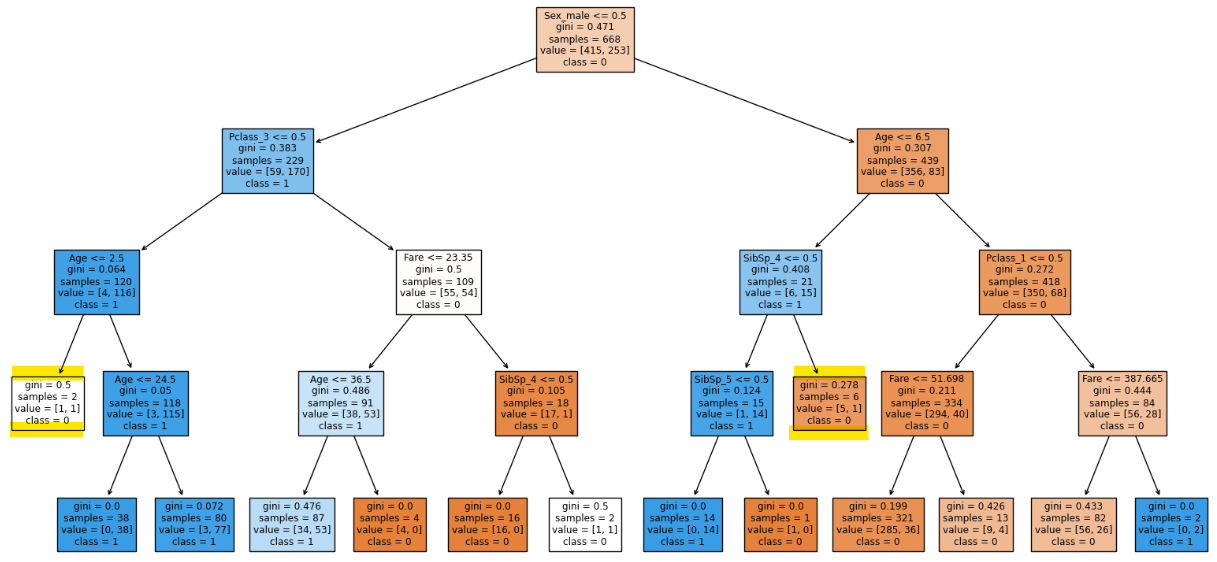
There’s a discount of two leaf nodes. 

clf = DecisionTreeClassifier(max_depth = 4, min_samples_split = 16, random_state=0)
clf.match(X_train, y_train)
clf.rating(X_train, y_train), clf.rating(X_test, y_test)

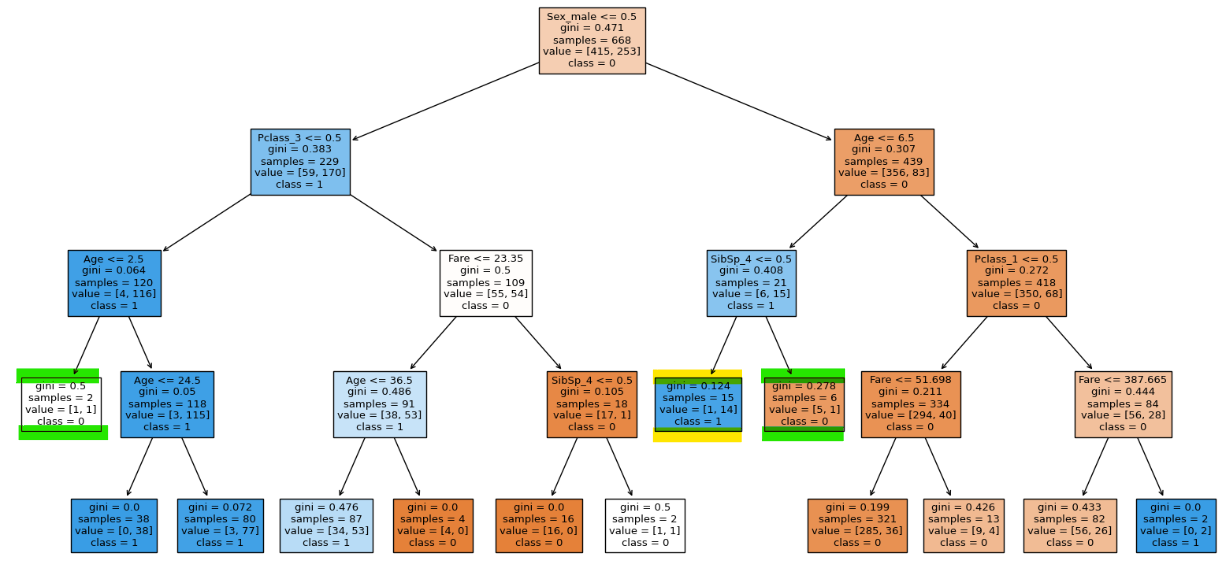
We are able to see that the highlighted node will not be splitting due to our hyper parameter.

clf = DecisionTreeClassifier(max_depth = 4, min_samples_split = 19, random_state=0)
clf.match(X_train, y_train)
clf.rating(X_train, y_train), clf.rating(X_test, y_te

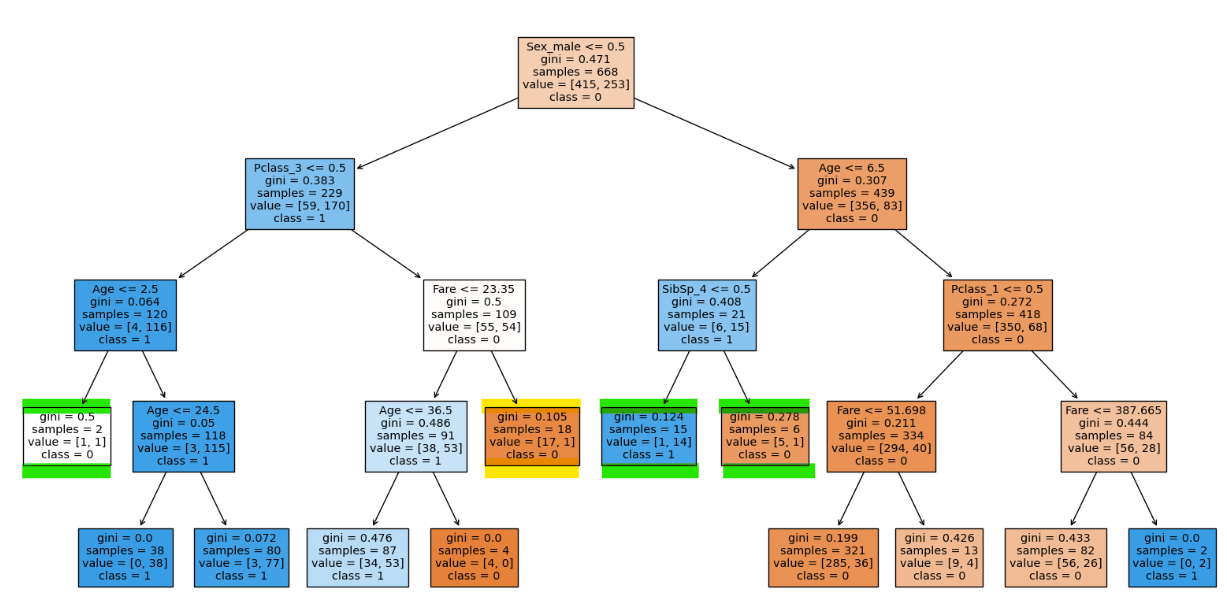
With min_samples_split 19 we are able to see that there’s much more leaf nodes decreased with much less compromise in testing accuracy. 

Occam’s razor is a precept typically attributed to. 14th–century friar William of Ockham says that if in case you have two competing concepts to elucidate the identical phenomenon, it is best to desire the easier one.

We are able to see that with only a drop of 0.2% in accuracy we are able to get an easier mannequin therefore we are able to go together with the extra generalized mannequin than a fancy one.  Additional enhance within the min_samples_split generalizes the mannequin inflicting it to underfit. Therefore having min_samples_split 19 will make our mannequin extra easier.

Step 10: Utilizing the Hyper Parameter

Utilizing the hyper parameter min_samples_leaf. A standard guideline to the full variety of samples in leaf nodes is ready to 1% to five%. Let’s go together with the identical and take a look at some tuning. 

Our dataset comprises 668 knowledge factors therefore 5% of it might be approx 35 we’ll strive min_sample_leaf to be 35.

clf = DecisionTreeClassifier(max_depth = 4, min_samples_split = 19,
min_samples_leaf = 35, random_state=0)
clf.match(X_train, y_train)
clf.rating(X_train, y_train), clf.rating(X_test, y_test)

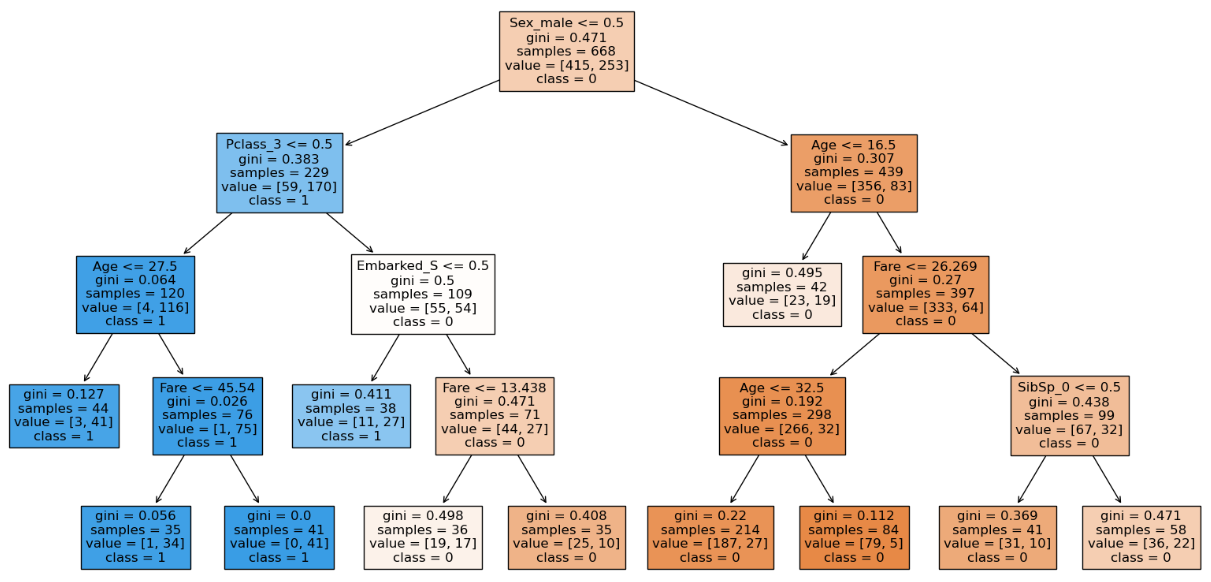
Right here we are able to see that with the rise within the min_samples_leaf to 35 the coaching accuracy decreases however testing accuracy doesn’t which suggests our mannequin can deal with unseen knowledge although the coaching accuracy is much less. We are able to additionally see that the construction of the choice tree is completely different than earlier than which has generalized. Therefore we’ll stick to min_samples_leaf of 35. We are able to see that the variety of nodes have decreased which suggests the mannequin has been generalized.

Step 11: Working with max_leaf_nodes has proven us that with enhance within the max_leaf_nodes till 6 has proven a optimistic affect the place after 6 there was no change within the validation accuracy.

clf = DecisionTreeClassifier(max_depth = 4, min_samples_split = 19,
min_samples_leaf = 35, max_leaf_nodes = 6, random_state=0)
clf.match(X_train, y_train)
clf.rating(X_train, y_train), clf.rating(X_test, y_test)

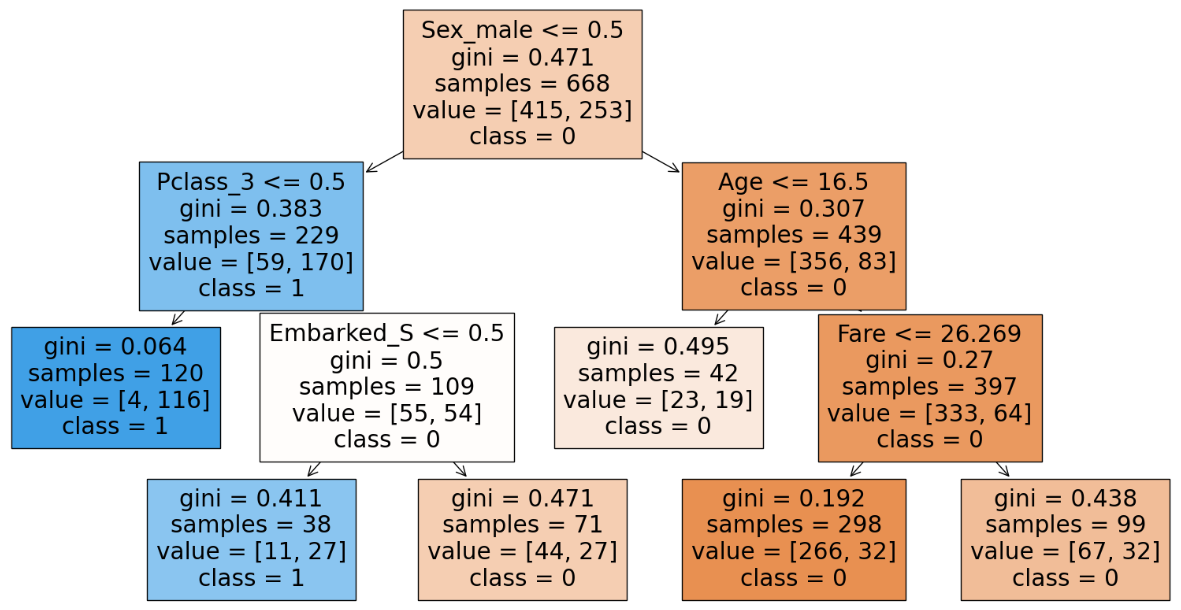
We are able to infer that with occum’s razor that with an easier mannequin we get the identical accuracy therefore we’ll go together with the easier mannequin and have max_leaf_nodes as 6.

Step 12: Work with max_features

Now lets work with max_features; default none.

clf = DecisionTreeClassifier(max_depth = 4, min_samples_split = 19,
min_samples_leaf = 35, max_leaf_nodes = 6, max_features = “log2”, random_state=0)
clf.match(X_train, y_train)
clf.rating(X_train, y_train), clf.rating(X_test, y_test)

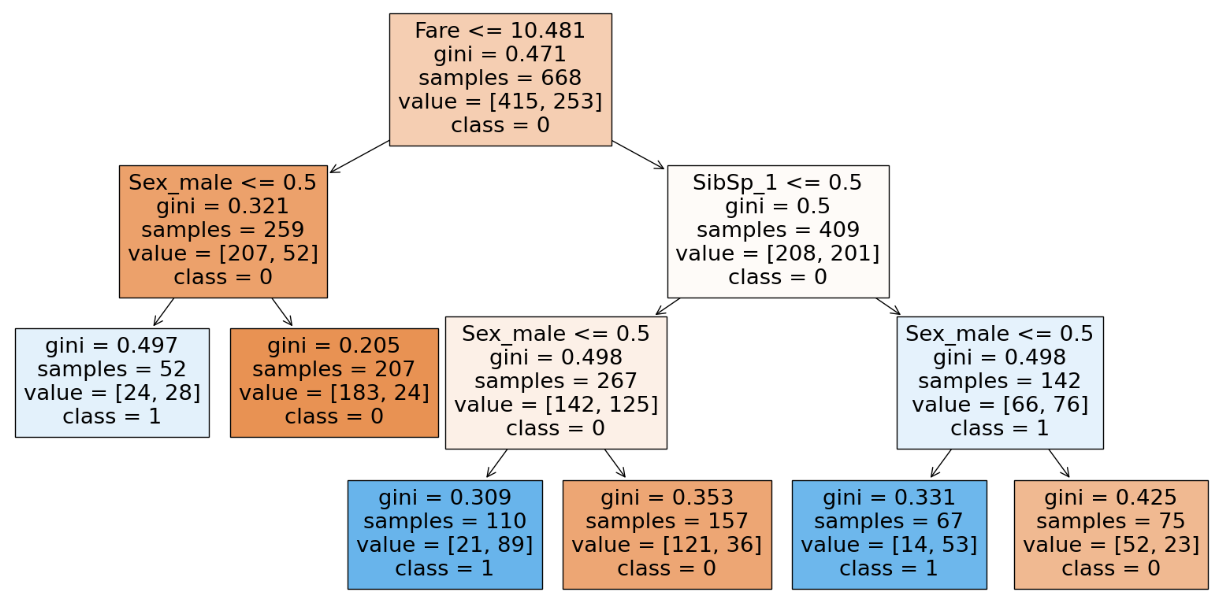
With the utilization of max_feature we are inclined to lower the coaching accuracy as we give much less options to work with. It will occur solely once we work with a dataset containing much less options however when working with massive datasets with a whole bunch of options utilizing max_features will assist because it reduces the computation to pick the function for the break up. We are able to infer from the parameter(variety of nodes) of the DT and notice that we try to generalize(lower in accuracy) much more because the nodes lower drastically. Therefore there’s a lower in accuracy and possibilities of underfitting.

Abstract of Hyper parameter tuning

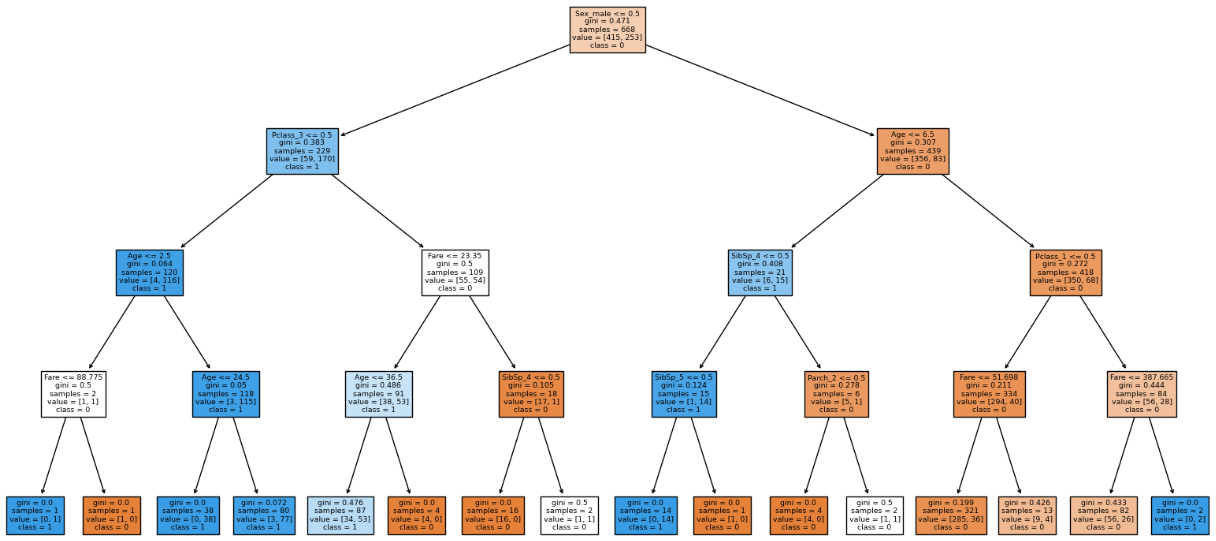
Visualization of Resolution Tree after Hyper Parameter Tuning

from sklearn.tree import plot_tree
import matplotlib.pyplot as plt

plt.determine(figsize=(20,10))  # Regulate the determine measurement as wanted
plot_tree(clf, crammed=True, feature_names=X_train.columns.tolist(),
class_names=clf.classes_.tolist())
plt.present()

This would be the construction of the choice tree after hyper parameter tuning. 

To know the hyper parameters of our determination tree:

params = clf.get_params()
print(params)

Conclusion

Resolution bushes characterize a cornerstone in machine studying, providing a clear and intuitive strategy to fixing classification and regression issues. By means of strategies like Data Acquire, Gini Impurity, Normal Deviation Discount, and Chi-Sq., determination bushes effectively partition datasets, making them invaluable throughout numerous domains.

This text supplied each theoretical insights and sensible implementation steering, enabling readers to assemble determination tree fashions from scratch utilizing Python and scikit-learn. By emphasizing the significance of hyperparameter tuning, readers gained proficiency in optimizing determination tree fashions for enhanced accuracy and generalization. Armed with this information, practitioners are poised to leverage determination bushes successfully in real-world purposes, making knowledgeable choices and driving impactful outcomes.

Often Requested Questions